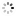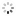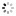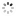Important Collectors Wristwatches, P...
Geneva, Mandarin Oriental Hotel Du Rhône, Oct 15, 2006
LOT 349
"Equation of Time - Ellicott Pendulum" Damiens Duvillier, Paris. Made circa 1850. Very fine, very rare and elegant, mahogany, month going, weight-driven floor standing precision regulator with equation of time, perpetual calendar, dead-center seconds, Ellicott-type pendulum with expansion indication.
CHF 60,000 - 80,000
EUR 38,000 - 50,000 / USD 50,000 - 65,000
Sold: CHF 82,600
C. Rectangular, mahogany, stepped and molded cornice, glazed sides and front door, canted corners, molded and canted plinth and kickboard. D. Matte silvered with radial Roman numerals, outer minute track, inner semi-circular scale for the equation of time inscribed "le soleil retarde - le soleil avance", annular silvered rotating year calendar dial below engraved with the months and baton divisions for the number of days in each month, the equation cam displayed in its center, molded gilt brass bezel. Gilt brass "Breguet" hour and minute hands, blued steel equation hand with gilt sun terminal. M. Massive, rectangular, gilt brass, the flat rectangular lead weight descending in a separate compartment behind the backboard, barrel with Harrison's maintaining power, fivewheel train, deadbeat escapement mounted on the backplate, the anchor with fine depthing adjustment and jeweled pallets, crutch with length adjustment and micrometer beat adjustment, Ellicott-type grid-iron pendulum with two brass rods and one steel rod, suspended from a massive rectangular brass plate fixed to the backboard, massive brass bob with semi-circular silvered scale above indicating the expansion or contraction of the brass pendulum rods and engraved "Elementa Suis Prepuis Amis Victa", the center of the bob with steel arms adjusted by screws in the side for altering the degree of compensation. Dial signed. Dim. 211 x 59 x 34.5 cm.
| Grading System | |
|---|---|
Grade: |
|
Case: 3 |
Good |
Movement: 2 |
Very good |
Dial: 3-01 |
Good HANDS Original |
Notes
Damiens Duvillier
Exhibited his regulators at the Great Exhibition, London, 1851 and the Exposition Universelle in Paris 1861.
Ellicott Pendulum
John Ellicott (1706 - 1772) was the inventor of a compensation pendulum in which the bob rests on the longer ends of two levers, of which the shorter ends are depressed by the superior expansion of the brass rods attached to the central steel pendulum rod.
Equation of Time due to Unequal Motion (the Earth's elliptical orbit)
The orbit of the Earth around the Sun is an ellipse. The distance between the Earth and the Sun is at a minimum around December 31 and is greatest around July 1. The Sun's apparent longitude changes fastest when the Earth is closest to the Sun. The Sun will appear on the meridian at noon on these two dates and so the Equation of Time due to Unequal Motion will then be zero. The mean solar day, calculated by averaging all the days of the year, was invented by astronomers for convenience so that the solar day would always be 24 hours. True solar time and mean solar time coincide four times a year, on April 16, June 14, September 1, and December 25. On these days, the equation will equal zero. During the other 361 days, the equation of time must be used to indicate the difference between the two times, amounting over 16 minutes at certain times of year. The minimum difference occurs on November 1 with a loss of 16 minutes and 23 seconds and the maximum occurs on February 11 with an increase of 14 minutes 20 seconds. This positive and negative value is offset in the time of the local noon and those of sunrise and sunset. Equation of time, often represented by a figure eight, called an ?analemma?, can be approximated by the following formula: E = 9.87 * sin (2B) - 7.53 * cos (B) - 1.5 * sin (B) Where: B = 360 * (N-81) / 365 Where: N = day number, January 1 = day 1.