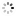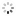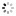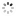Important Collectors Wristwatches, P...
Geneva, Mandarin Oriental Hotel Du Rhône, Oct 15, 2006
LOT 194
"Equation of Time" French. Made for the Indian market, imported by Favre Leuba & Co., Bombay, circa 1870. Fine and rare, gilt bronze and porcelain mounted, astronomic, 8-day going mantel clock with hour and halfhour striking, triple date, equation of time indication, moon phases and visible Brocot escapement.
CHF 8,000 - 10,000
EUR 5,000 - 6,500 / USD 6,500 - 8,000
Sold: CHF 17,700
C. Oval, gilt bronze decorated with scrolls, flowers and foliage, oak and laurel surmount with ribbon cresting, set with panels of faux Sevres porcelain decorated with putti emblematic of the four seasons, raised on gadrooned toupie feet. D. Two-piece, annular white enamel with radial Roman numerals, outer minute divisions, sunken centre with visible Brocot escapement, dial below with annular white enamel dial for the months and equation of time, sun symbols indicating the dates where solar and meantime are equal, sunken center with subsidiary dials for the days of the week and date, aperture for the moon phases. Black Breguet hands. M. 85 mm., circular, brass, going barrels for the going and striking trains, Brocot escapement with jeweled pallets, spring suspension, brass-bob pendulum, striking the hours and half-hours on a bell, patent calendar and equation of time movement below geared to the clock movement by a pinned wheel, manual adjustments for the days of the week, date and moon phase. Movement signed by the importer. Dim. 43.5 x 31 x 16 cm.
| Grading System | |
|---|---|
Grade: AA |
Very good |
Case: 3 |
Good |
Movement: 3* |
Good Overhaul recommended, at buyer's expense |
Dial: 3-45-01 |
Good HANDS Original |
Notes
Equation of Time due to Unequal Motion (the Earth's elliptical orbit).
The orbit of the Earth around the Sun is an ellipse. The distance between the Earth and the Sun is at a minimum around December 31 and is greatest around July 1. The Sun's apparent longitude changes fastest when the Earth is closest to the Sun. The Sun will appear on the meridian at noon on these two dates and so the Equation of Time due to Unequal Motion will then be zero. The mean solar day, calculated by averaging all the days of the year, was invented by astronomers for convenience so that the solar day would always be 24 hours. True solar time and mean solar time coincide four times a year, on April 16, June 14, September 1, and December 25. On these days, the equation will equal zero. During the other 361 days, the equation of time must be used to indicate the difference between the two times, amounting to over 16 minutes at certain times of the year. The minimum difference occurs on November 1 with a loss of 16 minutes and 23 seconds and the maximum occurs on February 11 with an increase of 14 minutes 20 seconds. This positive and negative value is offset in the time of the local noon and those of sunrise and sunset. Equation of time, often represented by a figure eight, called an ?analemma?, can be approximated by the following formula: E = 9.87 * sin (2B) - 7.53 * cos (B) - 1.5 * sin (B) Where: B = 360 * (N-81) / 365 Where: N = day number, January 1 = day 1.